
PPT Concavity and the Second Derivative Test PowerPoint Presentation - If f ''(x) < 0 for. Explain the concavity test for a function over. We conclude that we can determine the concavity of a function f by looking at the second derivative of f. If f > 0, then f has a relative minimum at (c,f(c)). Concavity and the second derivative test. You should also read this: Force Factor Test X180 Legend

PPT Understanding Concavity and Second Derivative Test PowerPoint - If f > 0, then f has a relative minimum at (c,f(c)). Let’s now investigate how concavity is determined by the sign of the second derivative. The second derivative test provides a means of classifying relative extreme values by using the sign of the second derivative at the. In this section we use second derivatives to determine the open intervals. You should also read this: Rmv Test Simulator

PPT Section 3.4 Concavity and the Second Derivative Test PowerPoint - Explain the concavity test for a function over. This is where the concepts of concavity and the second derivative come into play. Now, summarize your notes here! Use the second derivative test to find the relative extrema. Find the second derivative of and discuss the concavity of its graph. You should also read this: Calendar Synesthesia Test

PPT Concavity and the Second Derivative Test PowerPoint Presentation - If f ''(x) > 0 for all x in i , then the graph of f (x) is concave upward on i. If f > 0, then f has a relative minimum at (c,f(c)). To determine whether f ′ is increasing or decreasing on an interval, the easiest thing to do is look at its derivative, that is f ′′. You should also read this: Yeoman's Test
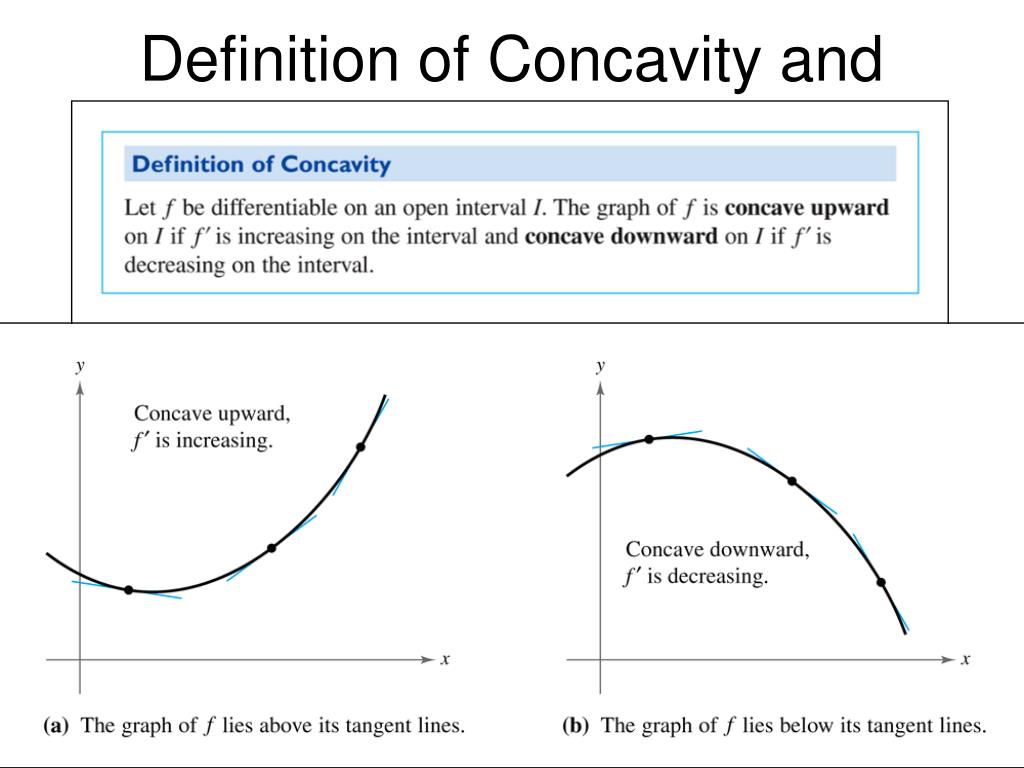
PPT CHAPTER 3 SECTION 3.4 CONCAVITY AND THE SECOND DERIVATIVE TEST - Explain the concavity test for a function over an open interval. Learn how the second derivative test determines intervals of concavity, locates inflection points, and identifies relative (local) extrema. Apply the second derivative test to find relative extrema of a function. If f > 0, then f has a relative minimum at (c,f(c)). This is where the concepts of concavity. You should also read this: Battery Tester Nearby

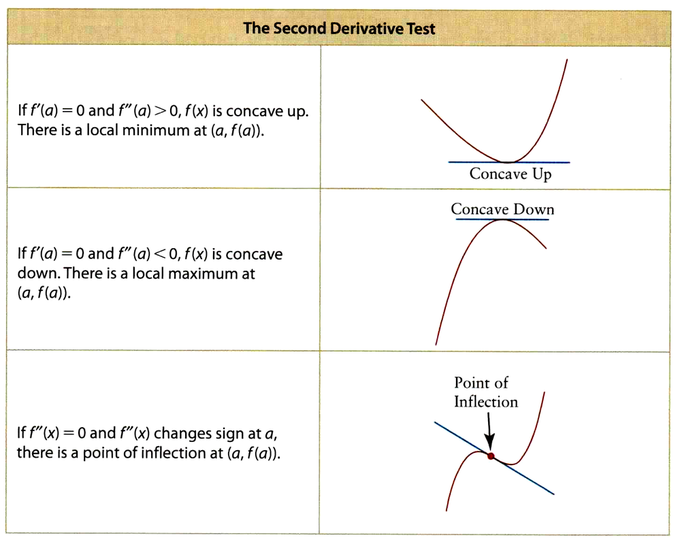
PPT Concavity and the Second Derivative Test PowerPoint Presentation - Concavity and the second derivative test. Second derivative test let f be a function such that f '(c) = 0 and the second derivative off exists on an open interval containing c. Do a sign analysis of second derivative to find intervals where f is concave up or down. We conclude that we can determine the concavity of a function. You should also read this: Ihealth Covid Test Near Me
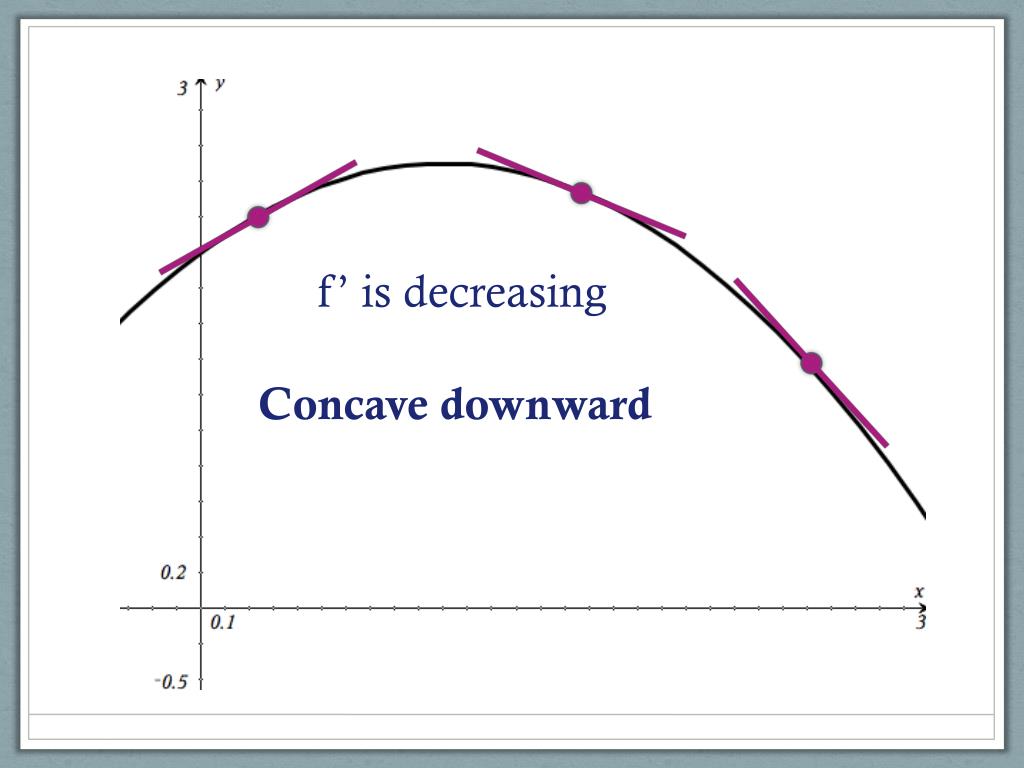
PPT Concavity and the Second Derivative Test PowerPoint Presentation - We have found intervals of increasing and decreasing, intervals where the. In this section we use second derivatives to determine the open intervals on which graphs of functions are concave up and on which they are concave down, to find inflection. To determine whether f ′ is increasing or decreasing on an interval, the easiest thing to do is look. You should also read this: Common Admission Test Wiki

1 2 Sec 4.3 Concavity and the Second Derivative Test ppt download - Test for concavitylet f(x) be a function whose second derivative exists on an open interval i. Understanding how a function behaves is crucial, especially around critical points. If f > 0, then f has a relative minimum at (c,f(c)). The second derivative test provides a means of classifying relative extreme values by using the sign of the second derivative at. You should also read this: Concussion Wise Test Answers
Section 3.3 GHCI Grade 12 Calculus & Vectors - Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Now, summarize your notes here! Apply the second derivative test to find relative extrema of a function. Do a sign analysis of second derivative to find intervals where f is concave up or down. Below is a picture that. You should also read this: Black Hand Holding A Positive Pregnancy Test
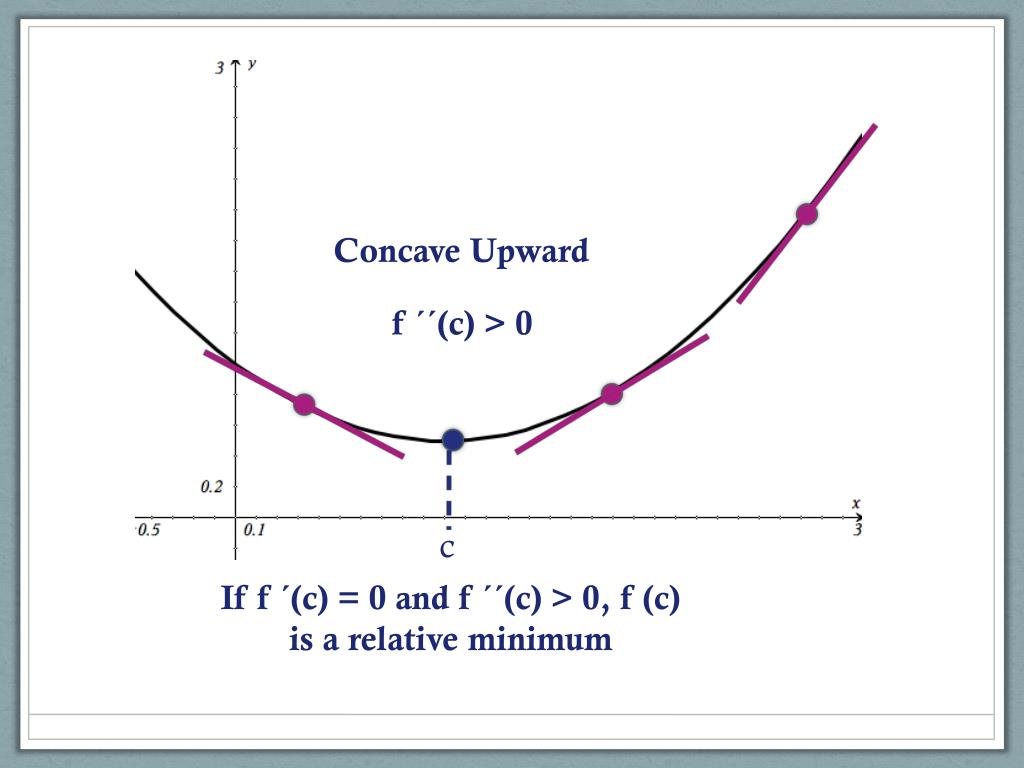
PPT Concavity and the Second Derivative Test PowerPoint Presentation - Concavity and the second derivative test. You have already seen that locating the intervals in which a function f increases or decreases helps to describe its graph. Use the second derivative test to find the relative extrema. In this section we use second derivatives to determine the open intervals on which graphs of functions are concave up and on which. You should also read this: Gothic Literature Mastery Test