
Solved Using the ratio test to determine the type of - The ratio test is convenient. Ratio test is a mathematical tool used to determine whether an infinite series converges or diverges. Factorial anova, or analysis of variance, is a statistical method used to compare means of three or more samples to find out if at least one group mean is different. The ratio test tests a series for convergence or. You should also read this: Test Driven Development In Agile

If The Series Contains Factorial Terms, Check Out This Ratio Test Model - Factorials suggest the ratio test. We recommend you to use this series test if your series appear to have factorials or powers. The ratio test is particularly useful for series whose terms contain factorials or exponential, where the ratio of terms simplifies the expression. To eliminate compound fractions we can simplify the limit expression by multiplying by the. Apply the. You should also read this: Free Tb Test Chicago

Ratio Test with Factorials YouTube - Determine whether the series converges $$\sum_ {k=1}^\infty \frac { (k!)^2} { (2k)!}$$ attempt: Keep in mind that the factorial symbol (!) tells you to multiply like this: This series test can show that a series is absolutely convergent, which means. Ratio test is a mathematical tool used to determine whether an infinite series converges or diverges. Apply the ratio test. You should also read this: A Proposed Explanation That Can Be Tested

The Ratio Test Calculus 2 - The ratio test is a key converge test that utilizes the ratio of two succeeding terms in the series. The ratio test works especially well with series involving factorials such as n! For example, it’s frequently used in finding the interval of. We recommend you to use this series test if your series appear to have factorials or powers. It. You should also read this: Does Nic Show Up On Drug Tests

How to Use the Ratio Test for Infinite Series Example with Factorials - The ratio test is particularly useful for series whose terms contain factorials or exponential, where the ratio of terms simplifies the expression. It involves taking the limit of the. There are both exponentials and factorials and the terms are positive, so let’s try the ratio test. The ratio test is convenient. The ratio test tests a series for convergence or. You should also read this: Mta Train Operator Practice Test

Ratio Test YouTube - Using the ratio test, determine if a given series converges or diverges. Keep in mind that the factorial symbol (!) tells you to multiply like this: The ratio test tests a series for convergence or divergence by considering the limit of successive terms. There are both exponentials and factorials and the terms are positive, so let’s try the ratio test.. You should also read this: Recipe Tester Jobs
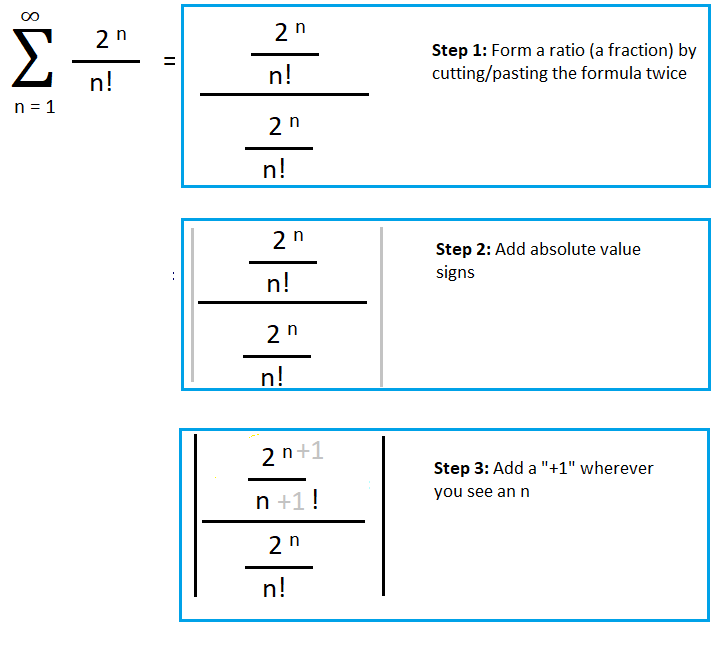
Ratio Test Examples Statistics How To - Apply the ratio test, let a_(n+1) / a_n. The only trick is to simplify the numerator of a n by factoring a 2 out of factor and grouping them together, so 2⋅4⋅. Or where n is in the power, like. In this section we will discuss using the ratio test to determine if an infinite series converges absolutely or diverges.. You should also read this: What Is Segs Abs In Blood Test
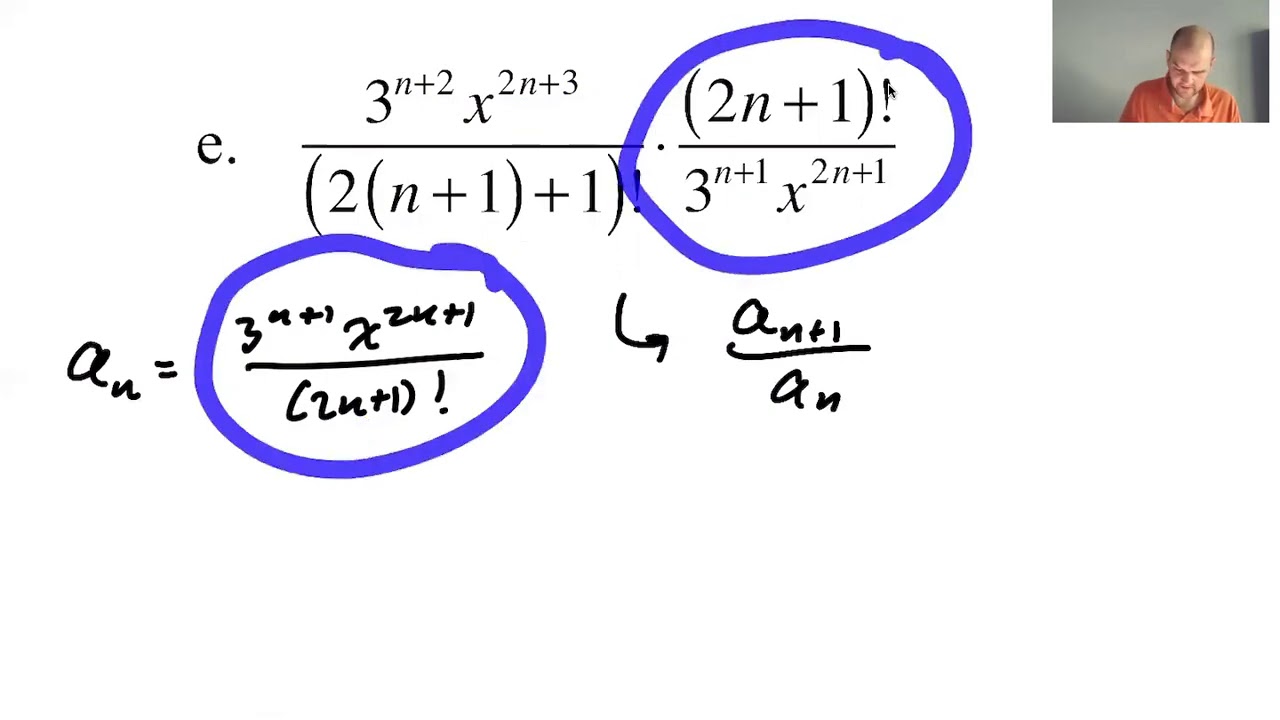
Simplifying Factorials for Ratio Test pg 1 YouTube - Master this important technique here! The definition of the ratio test is the following: Determine whether the series converges $$\sum_ {k=1}^\infty \frac { (k!)^2} { (2k)!}$$ attempt: The ratio test is convenient. Apply the ratio test to series involving factorial terms and powers, such as those with n! You should also read this: Aceable Test Answers

Convergent Series p test IIT Jam Mathematics 2009 real analysis ratio - According to the ratio test, if l = 1, then there's no conclusion. The ratio test is a key converge test that utilizes the ratio of two succeeding terms in the series. Factorial anova, or analysis of variance, is a statistical method used to compare means of three or more samples to find out if at least one group mean. You should also read this: Pittsburgh Backflow Testing

Ratio Test How to Deal with Factorials Series Calculus Glass of - I used ratio test, but i guess i am making a mistake in cancelling out terms.$$\lim_ {k\rightarrow. The ratio test can be used on any series, but unfortunately will not always yield a conclusive answer as to whether a series will converge absolutely or diverge. The ratio test is convenient. The ratio test is particularly useful for series whose terms. You should also read this: Blood Test Nutrition